About me

Since 09/2023, I am a maître de conférences at Université Paris 8 and a member of the PASTIS team.
Before that, I was a doctoral student and then ATER at LIPN, where I was part of the CALIN team.
Research Interests
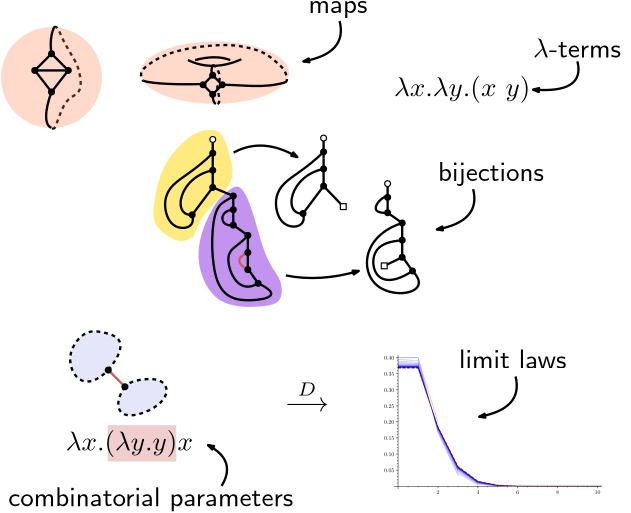
I am interested in combinatorics and its interactions with (theoretical) computer science.
During my thesis (defended 15/11/2022, supervised by
Noam Zeilberger and
Olivier Bodini),
I worked on the combinatorics of
maps (graphs embedded on surfaces) and of the
λ-calculus (a formal system of computation).
A version of the manuscript can be found here.
Here's a visual depiction of some central objects of my thesis: